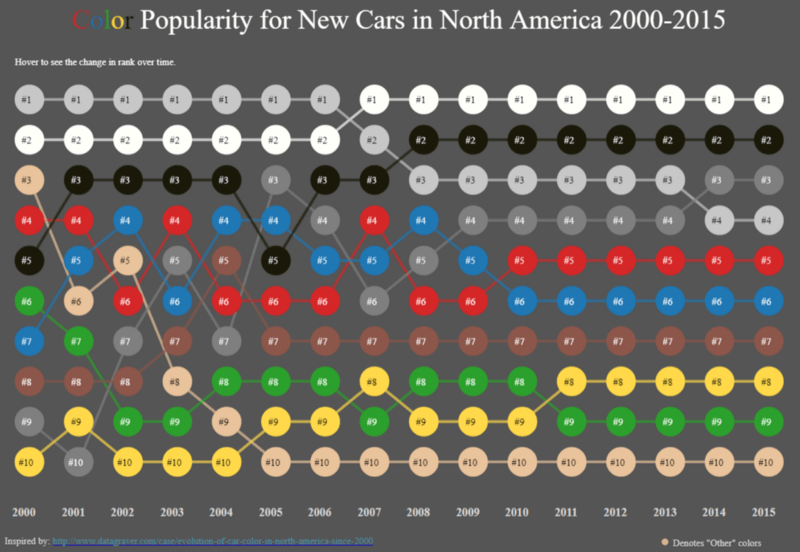
ANOVA is a general technique that can be used to test the hypothesis that the means among two or more groups are equal, under the assumption that the sampled populations are normally distributed.
Suppose we wish to study the effect of temperature on a passive component such as a resistor. We select three different temperatures and observe their effect on the resistors. This experiment can be conducted by measuring all the participating resistors before placing resistors each in three different ovens. Each oven is heated to a selected temperature. Then we measure the resistors again after, say, 24 hours and analyse the responses, which are the differences between before and after being subjected to the temperatures. The temperature is called a factor. The different temperature settings are called levels. In this example there are three levels or settings of the factor Temperature.
A factor is an independent treatment variable whose settings (values) are controlled and varied by the experimenter. The intensity setting of a factor is the level. Levels may be quantitative numbers or, in many cases, simply “present” or “not present” (“0” or “1”). For example, the temperature setting in the resistor experiment may be:100 degree F, 200 degree F and 300 degree F. We can simply call them: Level1, Level 2 and Level 3
The 1-way ANOVA
In the experiment above, there is only one factor, temperature, and the analysis of variance that we will be using to analyse the effect of temperature is called a one-way or one-factor ANOVA.
The 2-way or 3-way ANOVA
We could have opted to also study the effect of positions in the oven. In this case there would be two factors, temperature and oven position. Here we speak of a two-way or two-factor ANOVA. Furthermore, we may be interested in a third factor, the effect of time. Now we deal with a three-way or three-factor ANOVA. In each of these ANOVA’s we test a variety of hypotheses of equality of means (or average responses when the factors are varied).
ANOVA is defined as a technique where the total variation present in the data is portioned into two or more components having specific source of variation. In the analysis, it is possible to attain the contribution of each of these sources of variation to the total variation. It is designed to test whether the means of more than two quantitative populations are equal. It consists of classifying and cross-classifying statistical results and helps in determining whether the given classifications are important in affecting the results.
The assumptions in analysis of variance are:
Normality
Homogeneity
Independence of error
Whenever any of these assumptions is not met, the analysis of variance technique cannot be employed to yield valid inferences.
With analysis of variance, the variations in response measurement are partitioned into components that reflect the effects of one or more independent variables. The variability of a set of measurements is proportional to the sum of squares of deviations used to calculate the variance:
Σ(X-x ̅)2
Analysis of variance partitions the sum of squares of deviations of individual measurements from the grand mean (called the total sum of squares) into parts: the sum of squares of treatment means plus a remainder which is termed the experimental or random error.
When an experimental variable is highly related to the response, its part of the total sum of the squares will be highly inflated.
This condition is confirmed by comparing the variable sum of squares with that of the
random error sum of squares using an F test.
Why use Anova and Not Use t-test Repeatedly?
The t-test, which is based on the standard error of the difference between two means, can only be used to test differences between two means
With more than two means, could compare each mean with each other mean using t tests
Conducting multiple t-tests can lead to severe inflation of the Type I error rate (false positives) and is NOT RECOMMENDED.
ANOVA is used to test for differences among several means without increasing the Type I error rate
The ANOVA uses data from all groups to estimate standard errors, which can increase the power of the analysis
Why Look at Variance When Interested in Means?
Three groups tightly spread about their respective means, the variability within each group is relatively small
Easy to see that there is a difference between the means of the three groups
Three groups have the same means as in previous figure but the variability within each group is much larger
Not so easy to see that there is a difference between the means of the three groups
To distinguish between the groups, the variability between (or among) the groups must be greater than the variability of, or within, the groups
If the within-groups variability is large compared with the between-groups variability, any difference between the groups is difficult to detect
To determine whether or not the group means are significantly different, the variability between groups and the variability within groups are compared
One-Way ANOVA
Suppose there are k populations which are from a normal distribution with unknown parameters. A random sample X1, X2, X3……………… Xk is taken from these populations
which hold the assumptions. If μ1, μ2, μ3………… μk are k population means, the null hypothesis is:
H0 : μ1 = μ2 = μ3………… = μk (i.e. all means are equal)
HA : μ1 ≠ μ2 ≠ μ3………… ≠ μk (i.e. all means are not equal)
The steps in carrying out the analysis are:
Calculate variance between the samples
The variance between samples measures the difference between the sample mean of each group and the overall mean. It also measures the difference from one group to another. The sum of squares between the samples is denoted by SSB. For calculating variance between the samples, take the total of the square of the deviations of the means of various samples from the grand average and divide this total by the degree of freedom, k-1 , where k = no. of samples.
Calculate variance within samples
The variance within samples measures the inter-sample or within sample differences due to chance only. It also measures the variability around the mean of each group. The sum of squares within the samples is denoted by SSW. For calculating variance within the samples, take the total sum of squares of the deviation of various items from the mean values of the respective samples and divide this total by the degree of freedom, n-k, where n = total number of all the observations and k = number of samples.
Calculate the total variance
The total variance measures the overall variation in the sample mean. The total sum of squares of variation is denoted by SST. The total variation is calculated by taking the squared deviation of each item from the grand average and dividing this total by the degree of freedom, n-1 where n = total number of observations.
Calculate the F ratio
It measures the ratio of between–column variance and within-column variance. If there is a real difference between the groups, the variance between groups will be significantly larger than the variance within the groups.
F = ( Variance between the Groups ) / Variance within the Groups
F = SSB / SSW
Decision Rule
At a given level of significance E =0.05 and at n-k and k-1 degrees of freedom, the value of F is tabulated from the table. On comparing the values, if the calculated value is greater than the tabulated value, reject the null hypothesis. That means the test is significant or there is a significant difference between the sample means.
Applicability of ANOVA
Analysis of variance has wide applicability from experiments. It is used for two different purposes:
It is used to estimate and test hypothesis about population means.
It is used to estimate and test hypothesis about population variances.
An analysis of variance to detect a difference in three or more population means first requires obtaining some summary statistics for calculating variance of a set of data as shown below: Where:
Σx2 is called the crude sum of squares
(Σx)2 / N is the CM (correction for the mean), or CF (correction factor)
Σx2 – (Σx)2 / N is termed SS (total sum of squares, or corrected SS).
σ2(variance)=(Total sum of squares)/(Total DF (Degrees of freedom))=(∑▒〖x^2-(〖∑▒x)〗^2/N〗)/(N-1)
In the one-way ANOVA, the total variation in the data has two parts: the variation among treatment means and the variation within treatments.
The grand average GM = Σx/N
The total SS (Total SS) is then:
Total SS = Σ(Xi – GM)2 Where Xi is any individual measurement.
Total SS = SST + SSE Where SST = treatment sum of squares and SSE is the experimental error sum of squares.
Sum of the squared deviations of each treatment average from the grand average or grand mean.
Sum of the squared deviations of each individual observation within a treatment from the treatment average. For the ANOVA calculations:
Total Treatment CM Σ(TCM)=
SST = Σ(TCM) – CM
SSE = Total SS – SST (Always obtained by difference)
Total DF = N – 1 (Total Degrees of Freedom)
TDF = K – 1 (Treatment DF = Number of treatments minus 1)
EDF = (N – 1) – (K – 1) = N – K (Error DF, always obtained by difference)
MST =SST/TFD=SST/(K-1) (Mean Square Treatments)
MSE = SSE/EDF=SSE/(N-K) (Mean Square Error)To test the null hypothesis:
H0 : μ1 = μ2 = μ3………… = μk H1 : At least one mean different
F = MST/MSE When F > Fα , reject H0The overall mean is
Two-Way ANOVA
It will be seen that the two-way analysis procedure is an extension of the patterns described in the one-way analysis. Recall that a one-way ANOVA has two components of variance: Treatments and experimental error (may be referred to as columns and error or rows and error). In the two-way ANOVA there are three components of variance: Factor A treatments, Factor B treatments, and experimental error (may be referred to as columns, rows, and error).
In a two way analysis of variance, the treatments constitute different levels affected by more than one factor. For example, sales of car parts, in addition to being affected by the point of sale display, might also be affected by the price charged, the location of store and the number of competitive products. When two independent factors have an effect on the dependent factor, analysis of variance can be used to test for the effects of two factors simultaneously. Two sets of hypothesis are tested with the same data at the same time.
Suppose there are k populations which are from normal distribution with unknown parameters. A random sample X1, X2, X3……………… Xk is taken from these populations which hold the assumptions. The null hypothesis for this is that all population means are equal against the alternative that the members of at least one pair are not equal. The hypothesis follows:
H0 : μ1 = μ2 = μ3………… = μk
HA : Not all means μj are Equal.
If the population means are equal, each population effect is equal to zero against the alternatives. The test hypothesis is
H0 : β1 = β2 = β3………… = βk
HA : Not all means βj are Equal.
Calculate variance between the rows
The variance between rows measures the difference between the sample mean of each row and the overall mean. It also measures the difference from one row to another. The sum of squares between the rows is denoted by SSR. For calculating variance between the rows, take the total of the square of the deviations of the means of various sample rows from the grand average and divide this total by the degree of freedom, r-1 , where r= no. of rows.
Calculate variance between the columns
The variance between columns measures the difference between the sample mean of each column and the overall mean. It also measures the difference from one column to another. The sum of squares between the columns is denoted by SSC. For calculating variance between the columns, take the total of the square of the
deviations of the means of various sample columns from the grand average and divide this total by the degree of freedom, c-1 , where c= no. of columns.
Calculate the total variance
The total variance measures the overall variation in the sample mean.The total sum of squares of variation is denoted by SST. The Total variation is calculated by taking the squared deviation of each item from the grand average and divide this total by degree of freedom, n-1 where n= total number of observations.
Calculate the variance due to error
The variance due to error or Residual Variance in the experiment is by chance variation. It occurs when there is some error in taking observations, or making calculations or sometimes due to lack of information about the data. The sum of squares due to error is denoted by SSE. It is calculated as:
Error Sum of Squares = Total Sum of Squares – Sum of Squares between Columns – Sum of Squares between Rows.
The degree of freedom in this case will be (c-1)(r-1).
Calculate the F Ratio
It measures the ratio of between–column variance and within-row variance with variance due to error.
F = Variance between the Columns / Variance due to Error
F = SSC / SSE
F = Variance between the Rows / Variance due to Error
F = SSR / SSE
Decision Rule At a given level of significance α=0.05 and at n-k and k-1 degrees of freedom, the value of F is tabulated from the table. On comparing the values, if the calculated value is greater than the tabulated value, reject the null hypothesis. This means that the test is significant or, there is a significant difference between the sample means.
ANOVA Table for an A x B Factorial Experiment
In a factorial experiment involving factor A at a levels and factor B at b levels, the total sum of squares can be partitioned into:
Total SS = SS(A) + SS(B) + SS(AB) + SSE
ANOVA Table for a Randomized Block Design
The randomized block design implies the presence of two independent variables, blocks and treatments. The total sum of squares of the response measurements can be partitioned into three parts, the sum of the squares for the blocks, treatments, and error. The analysis of a randomized block design is of less complexity than an A x B factorial experiment.
Goodness-of-Fit Tests
GOF (goodness-of-fit) tests are part of a class of procedures that are structured in cells. In each cell there is an observed frequency, (Fo). From the nature of the problem, one either knows the expected or theoretical frequency, (Fe) or can calculate it. Chi square (χ2) is then summed across all cells according to the formula:
The calculated chi square is then compared to the chi square critical value for the following appropriate degrees of freedom: